有限元分析一定可以得到问题的精确解吗?
理论上可以证明,如果插值函数使用了“协调和完整的位移函数”,则当网格尺寸逐渐减小而单元数量增加时,解就会单调收敛。
而且,当单元数目增加时,得到的刚度会降低,并收敛于真实刚度;这就意味着,当单元增加时,得到的位移增加,而收敛于精确位移解。其图形如下:
这里所说的“协调和完整位移函数”,是指:
1.近似函数式一般是多项式。
2.近似函数在单元内要保持连续。
3.近似函数应提供单元间的连续性,包括离散单元每一个节点所有自由度都应该是连续的,二维单元和三维单元沿着公共边界线和公共面必须是连续的。
既能够保证单元内的连续,又能够保证单元间的连续的形函数称为协调函数。
4.近似函数应考虑刚体位移和单元内的常应变状态。即有常数项保证刚体运动(无应变的运动),而有一次项保证有常应变状态发生。这是形函数的完整性问题。
例如,对于一维单元而言,若取形函数
则同时满足上面四个条件,称为协调且完整的位移函数。
一般来说,我们所用的单元使用的位移函数都满足上述四个条件,所以从理论上来说,只要网格加密,就可以收敛于真实解。
为了验证上述理论的真实性,我们选用了一个材料力学中的例子来做仿真。
该例子如下
使用材料力学的理论进行求解,简要过程如下
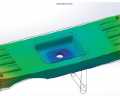
使用ANSYS进行分析,使用BEAM188单元,首先创建如图所示的几何模型
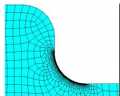
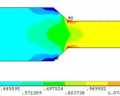
然后分别对各段直线加密网格划分,得到的结果如下
上表中,第一列是划分的单元数,第二列是最大的压应力,第三列是最大的拉应力。可以看到,随着单元数目的增加,最大拉伸,压缩应力的绝对值都在增加。
从材料力学得到的精确解,最大的压应力是-46.2MPa, 最大的拉应力是28.8MPa。这样,当单元数增加到64个时,压应力的误差是(46.2-45.7)/46.2 =1.1%; 拉应力的精度是(28.8-28.6)/28.8=0.7%.此时精度已经相当高了。
可以明显的看出,随着单元数目的增加,应力解的确是在逐渐逼近真实解。从这个方面来说,加密网格的确是提高计算精度的有效方法。
这也意味着,我们在有限元仿真中,如果要得到精确的结果,必须不断细分网格,直到结果收敛。否则,我们的得到结果就是不可信的。
那么,对于任何问题,只要网格无限细分,一定可以收敛于真实解吗?
未必。